私たちは量子力学と統計力学に立脚した物性理論の研究をおこなっています。
近年の物性研究において、物質中の電子を記述する波動関数の位相が示す幾何学的な(トポロジカルな)性質に着目することにより、物質の示す量子相についての深い知見が得られることが明らかになってきました。私たちは、量子物質のトポロジカルな側面に着目し、多様な量子相の対称性の観点からの理解と、それらが発現する特異な物理現象について研究をすすめています。特に、強相関物質や非線形応答・光学効果などに対して、非自明な波動関数の位相の構造がどのような物性現象として発現するかに興味を持って研究を行っています。研究手法としては、場の理論などの解析的な方法に、数値的な方法を織り交ぜながら研究を行っています。
具体的には、
- トポロジカル量子相(トポロジカル絶縁体、ワイル半金属の分類理論・電磁応答)
- 非線形光学効果、非線型伝導(シフト電流、非相反電流)
- 非平衡定常系(フロッケ理論・ケルディッシュグリーン関数)
を対象とした研究を行ってきました。
1. 幾何学位相に駆動された光起電力効果:シフト電流
非線形光学効果は長い研究の歴史をもち、高調波発生、光起電力、非線形カー回転といった応用上も重要な現象の宝庫です。近年の光起電力効果における特筆すべき発展のひとつに、反転対称性を欠いたペロブスカイト酸化物における高効率の光起電力効果(太陽電池効果)の発見があげられます。その高効率太陽電池効果のメカニズムとしてシフト電流と呼ばれる現象が提案されています。シフト電流は、従来のpn接合における光起電力効果と異なり、反転対称性を破ったバルク結晶中で生じる太陽電池効果です。
これらの発展をうけて、私は非線形光学効果における幾何学的側面について研究を行いました。光の周期的電場を取り扱うフロッケ理論と、非平衡定常状態を記述するケルディッシュ・グリーン関数法を組み合わせることで、私は非線形光学応答の新しい定式化を整備しました [1]。この手法を用いると、光照射下で実現する非平衡定常状態を実効的なバンド描像により明快に記述することができます。これにより、シフト電流、第二高調波発生(SHG)といった非線形応答を、シフトベクトルというベリー位相に関連する量を用いて統一的に記述できることがわかりました。シフトベクトルは、光照射によるバンド間励起に伴う電子波束の実空間変位のことであり、現代的な分極理論と密接に結びついた幾何学的な量といえます。
さらに、固体中の準粒子励起もシフト電流機構により太陽電池効果を示すことが明らかになってきました。私たちはフロッケ理論や場の理論によるダイアグラム法などを用いて、これら準粒子励起のシフト電流の理論提案を行いました。例えば、光励起された電子と正孔の束縛状態である励起子は、反転対称性の破れた結晶中では中心位置のシフトにより電気分極を持ちます。これにより励起子は電荷中性であるにも関わらず光電流を運ぶことができることが明らかになりました[2]。この励起子シフト電流は実験的にも検証されています。同様のメカニズムにより、格子振動の準粒子であるフォノンや磁気励起の準粒子であるマグノンなども太陽電池効果の担い手となることが明らかになっています。
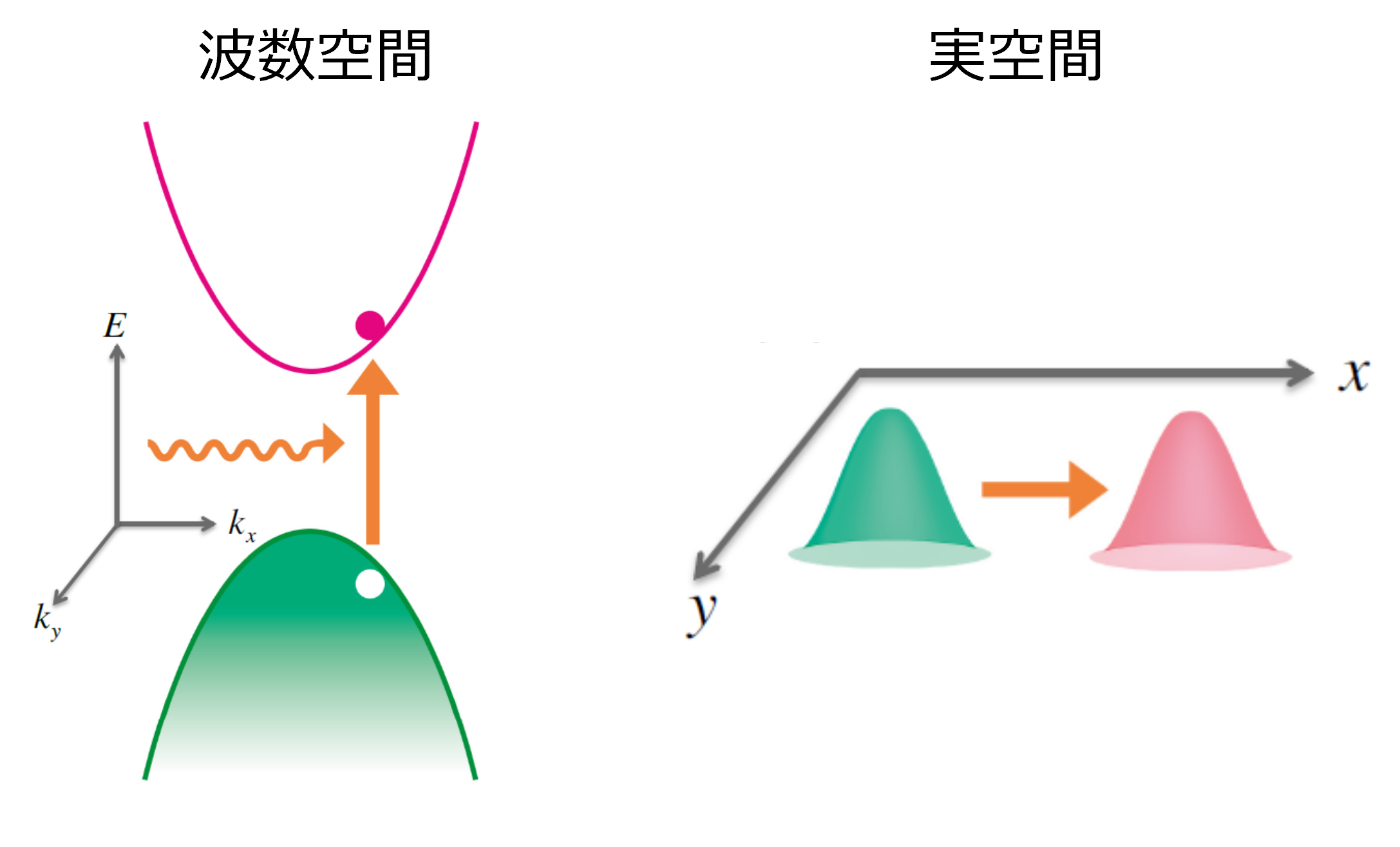
図、フロッケ理論による非線形光学応答の記述
[1] Takahiro Morimoto, Naoto Nagaosa, ” Topological nature of nonlinear optical effects in solids ” Science Advances 2, e1501524 (2016).
[2] Takahiro Morimoto, Naoto Nagaosa, ” Topological aspects of nonlinear excitonic processes in noncentrosymmetric crystals ” Phys. Rev. B 94, 035117 (2016).
[解説論文] Takahiro Morimoto, Sota Kitamura, Naoto Nagaosa, “Geometric Aspects of Nonlinear and Nonequilibrium Phenomena” J. Phys. Soc. Jpn. 92, 072001 (2023).
[講演スライド] Takahiro Morimoto, “Topological aspects of nonlinear optical effects” APS March Meeting 2018 (Y05.00004)
2. トポロジカル絶縁体の分類理論とその応用
トポロジカル絶縁体は、物質中の電子の波動関数が非自明な幾何学構造を持ち、それに伴って絶縁体の表面に安定なギャップレス励起が現れる物質群です。波動関数の幾何構造に由来する特有の非散逸的な応答現象を示し、その発見以来工学的な応用を目標として精力的に研究されています。最近では、トポロジカル絶縁体に加え、トポロジカル結晶絶縁体やワイル・ディラック半金属といった新たなトポロジカル相を実現する物質群が発見されたことで、トポロジカル量子相の研究は現在の物性研究のひとつのハイライトとなっています。
従来のトポロジカル絶縁体の分類理論では扱える対称性の種類が限られていましたが、私はクリフォード代数の表現論とK理論という数学的な手法を用いて分類理論を整備しなおすことにより、より一般の対称性をもつ系に適用可能なものに拡張しました [1]。このクリフォード代数による一般化された分類理論を応用することにより、私は以下のような研究を行ってきました。
- 鏡映対称性によって保護されたトポロジカル結晶絶縁体に対して一般化された分類理論を適用し、トポロジカル結晶絶縁体の分類表をえた [1]。
- ワイル・ディラック半金属に分類理論を適用することで、バルクギャップレス状態が結晶の対称性の下で安定化する条件や、新しい種類のギャップレス点が現れることを明らかにした [2,3,4]。
- 強い相互作用のもとでは、整数不変量をもつトポロジカル相が不安定化し、Z8といった有限群で特徴づけられることが知られている。私は、非線形シグマ模型とK理論を組み合わせることにより、強相関トポロジカル絶縁体の分類表を導出した [5]。
これらの分類理論は、対称性のもとで発現するトポロジカル量子相の系統的理解と、物質設計の指針を与えるものと考られます。
[1] Takahiro Morimoto, and Akira Furusaki, ” Topological classification with additional symmetries from Clifford algebras ” Phys. Rev. B 88, 125129 (2013).
[2] Takahiro Morimoto, and Akira Furusaki, ” Weyl and Dirac semimetals with Z2 topological charge ” Phys. Rev. B 89, 235127 (2014).
[3] Bohm-Jung Yang, Takahiro Morimoto, and Akira Furusaki, ” Topological charges of three-dimensional Dirac semimetals with rotation symmetry ” Phys. Rev. B 92, 165120 (2015).
[4] Bohm-Jung Yang, Troels Arnfred Bojesen, Takahiro Morimoto, and Akira Furusaki, ” Topological semimetals protected by off-centered symmetries in nonsymmorphic crystals ” Phys. Rev. B 95, 075135 (2017).
[5] Takahiro Morimoto, Akira Furusaki, and Christopher Mudry, ” Breakdown of the topological classification Z for gapped phases of noninteracting fermions by quartic interactions ” Phys. Rev. B 92, 125104 (2015).
[解説記事] 森本 高裕、古崎 昭 : ” トポロジカル絶縁体・超伝導体の分類理論とトポロジカル結晶絶縁体への応用, ” 固体物理 Vol. 50, No.6 (2015).
3.ワイル半金属におけるトポロジカルな非線形光学応答
ワイル半金属は物質の示すトポロジカルな量子相の一種です。ワイル半金属中では、結晶の周期ポテンシャルのために電子が線形分散の励起構造を示し、素粒子物理で存在が予言されている相対論的なワイル粒子と同様に振る舞うため興味がもたれています。線形分散の低エネルギー励起は波動関数の幾何学構造により安定的に存在し、それに伴ってフェルミアークと呼ばれる表面状態があらわれたり、ワイル粒子がもつカイラル異常という場の理論的性質から特異な電気的磁気的な応答現象を示したりします。
ワイル半金属の物性はこれまで線形応答現象を中心に調べられてきましたが、私たちはワイル半金属のトポロジカルな性質が非線形応答にどのようにあらわれるかに着目して研究を行いました。円偏光光起電力効果という非線形光学応答を調べると、線形分散励起を安定化する幾何学構造(ワイル点の周りでのベリー曲率積分の量子化)のために、物質の詳細によらず量子化するということがわかりました [1]。さらに、ワイル半金属の一般化である多重ワイル半金属というトポロジカル量子相が、RhSiといった物質中にあらわれることが知られています。私たちは多重ワイル半金属でも同様に円偏光光起電力効果が量子化を示すことを提案しました [2]。
また、代表的なワイル半金属物質としてTaAsが知られています。ワイル半金属TaAsにおいて第二高調波発生という非線形応答が、非常に大きくなる(可視光から赤外領域においてGaAsの100倍以上)ということが実験的にわかりました。私たちは非線形光学応答のフロッケ理論による定式化を用いて、巨大な第二高調波発生の理論解析を行いました。TaAsは空間反転対象の破れた結晶構造を持つためワイル半金属になることが知られていますが、第二高調波発生という空間反転対象が破れた系に特有の非線形応答もそれに伴って巨大になるということがわかりました [3]。 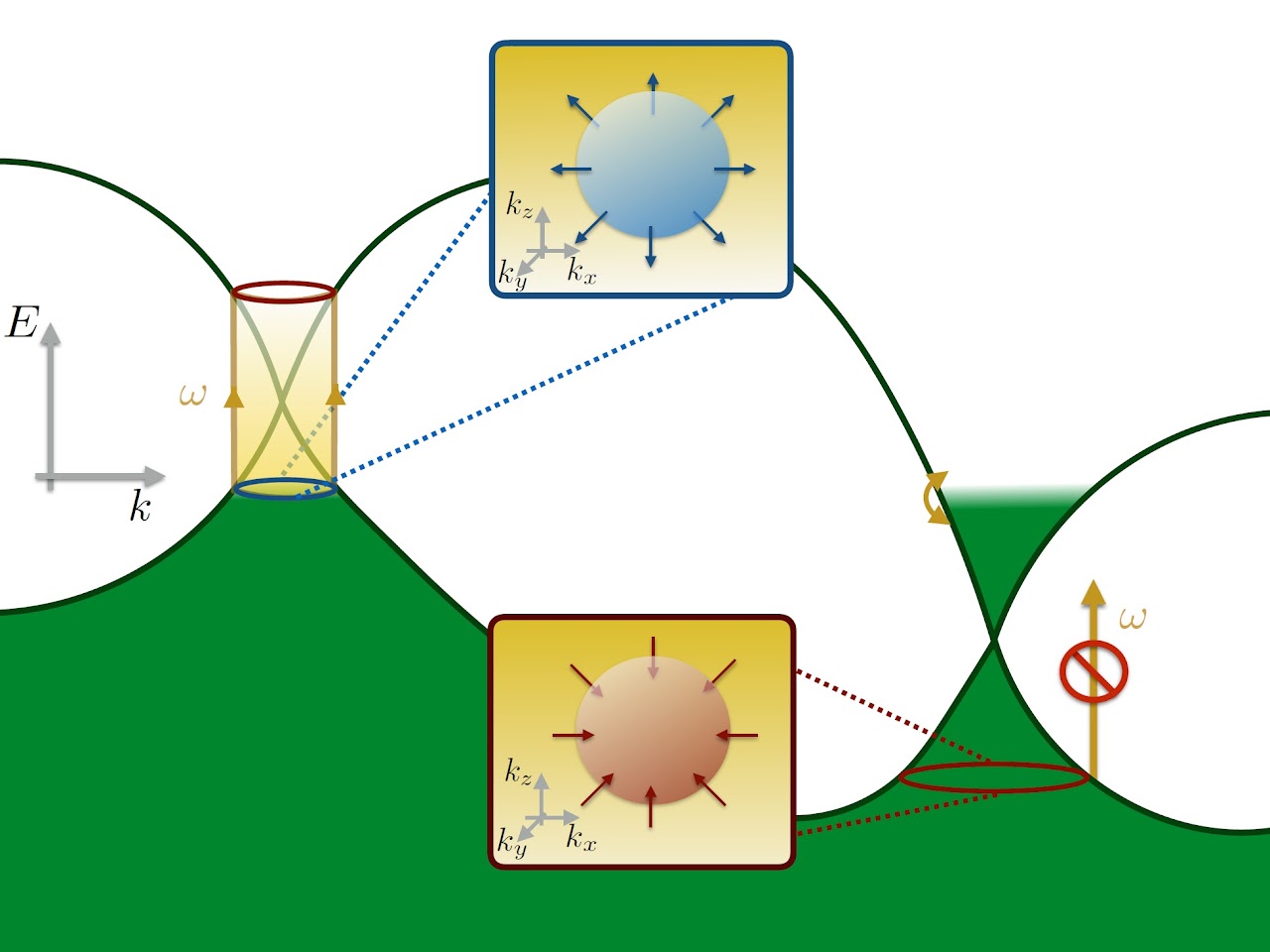
図、ワイル半金属における円偏光光起電力効果の量子化
[1] Fernando de Juan, Adolfo G. Grushin, Takahiro Morimoto, and Joel E. Moore: ” Quantized circular photogalvanic effect in Weyl semimetals ” Nature Communications 8, 15995 (2017).
[2] Felix Flicker, Fernando de Juan, Barry Bradlyn, Takahiro Morimoto, Maia G. Vergniory, and Adolfo G. Grushin: ” Chiral optical response of multifold fermions ” Phys. Rev. B 98, 155145 (2018). [3] Liang Wu, S. Patankar, T. Morimoto, N. L. Nair, E. Thewalt, A. Little, J. G. Analytis, J. E. Moore, J. Orenstein: ” Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals ” Nature Physics 13, 350 (2017).
4.非平衡定常系におけるフロッケ・トポロジカル相
周期的な外場(電場など)に駆動された非平衡定常系においては、平衡系では実現できないような新種のトポロジカル相が実現することが近年知られるようになり興味がもたれています。例えば、平衡状態ではトポロジカル相の代表例として量子ホール系がしられています。量子ホール系では、バルクのチャーン数と呼ばれるトポロジカル数と端に現れるギャップレス状態の数が対応している。一方で、非平衡定常系では、チャーン数がゼロであるにもかかわらず端にギャップレス状態が安定的に現れるフロッケ系を比較的簡単に構成することができます。このようなトポロジカル相は平衡状態では決して実現できない、非平衡系ならではの状態です。
私は、クリフォード代数の手法を用いて、一般のフロッケトポロジカル相の分類理論を構築しました。さらに、フロッケ系では時間並進と空間対称操作を組み合わせた動的な対称性(時間映進、時間らせん操作など)考えられるため、これらによって保護されたフロッケトポロジカル相の研究もおこないました [1]。
さらに、強い相互作用のもとで実現する強相関フロッケトポロジカル相についても研究をおこないました。コホモロジー理論と呼ばれる実効的なゲージ理論の分類理論を用いて、強相関フロッケトポロジカル相の分類理論を導出しました。またその知見に基づいて、1次元2次元の強相関フロッケトポロジカル相を実現する具体的なスピン模型を構築しました
[2,3]。
[1] Takahiro Morimoto, Hoi Chun Po, and Ashvin Vishwanath, ” Floquet topological phases protected by time glide symmetry ” Phys. Rev. B 95, 195155 (2017).
[2] Andrew C. Potter, Takahiro Morimoto, Ashvin Vishwanath, ” Classification of Interacting Topological Floquet Phases in One Dimension ” Phys. Rev. X 6, 041001 (2016).
[3] Andrew C. Potter and Takahiro Morimoto, ” Dynamically enriched topological orders in driven two-dimensional systems ” Phys. Rev. B 95, 155126 (2017).